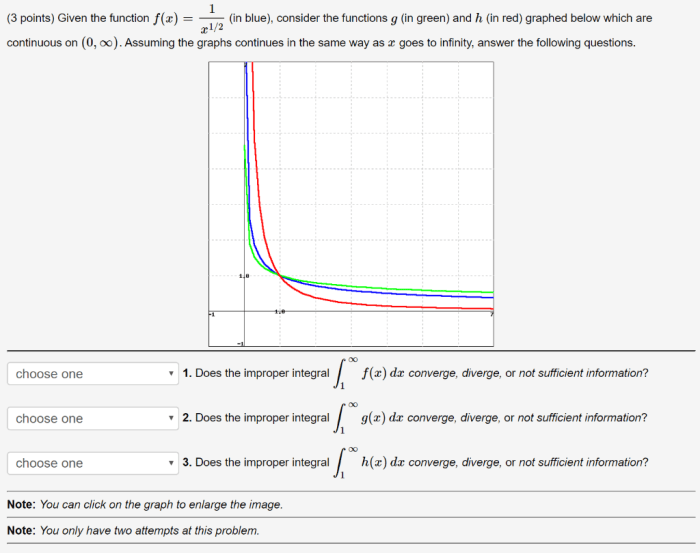
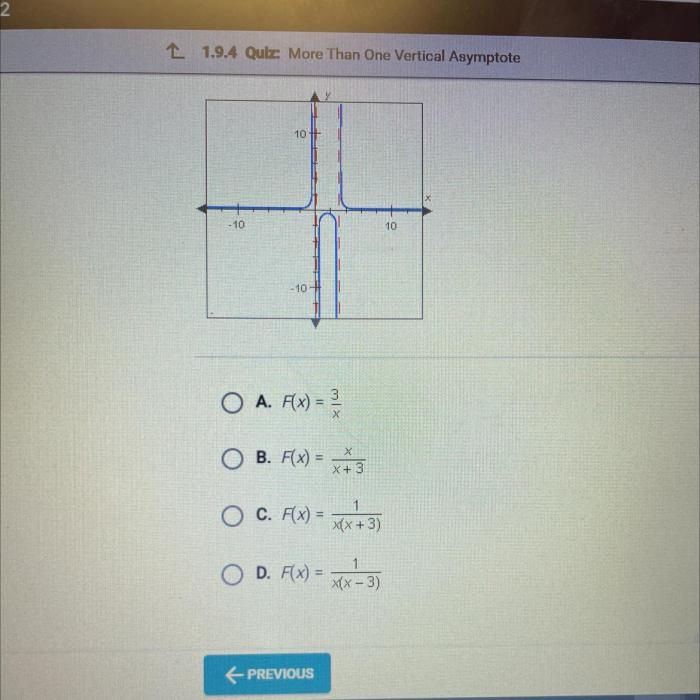
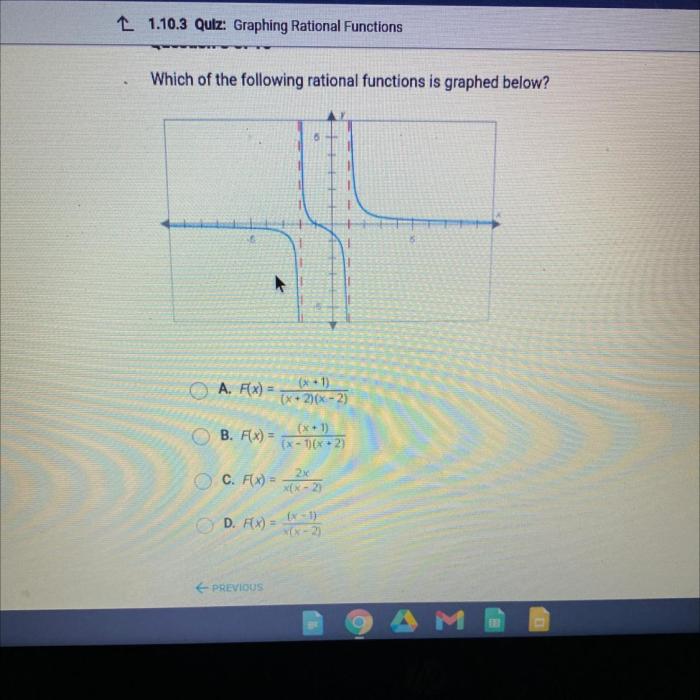
Which of the functions graphed below is continuous? This question delves into the fascinating world of mathematical continuity, where we explore the behavior of functions and their ability to flow smoothly without abrupt jumps or breaks. Join us on this journey as we uncover the secrets of continuity and its significance in various mathematical applications.
In this discourse, we will delve into the concept of continuous functions, examining their properties and characteristics. We will investigate different types of discontinuities, providing examples to illustrate their distinct behaviors. Furthermore, we will explore the process of analyzing functions for continuity, equipping you with the tools to determine whether a function is continuous or discontinuous at specific points.
Continuous Functions

A continuous function is one whose graph can be drawn without lifting the pen from the paper. In other words, there are no breaks or jumps in the graph.
Continuity can be defined in terms of limits and derivatives. A function is continuous at a point if the limit of the function as x approaches that point exists and is equal to the value of the function at that point.
Additionally, the derivative of a continuous function is also continuous.
Types of Discontinuities, Which of the functions graphed below is continuous
There are three main types of discontinuities: jump discontinuities, removable discontinuities, and infinite discontinuities.
- Jump discontinuity:A jump discontinuity occurs when the limit of the function exists, but it is not equal to the value of the function at that point. In other words, there is a “jump” in the graph of the function at that point.
- Removable discontinuity:A removable discontinuity occurs when the limit of the function exists, but the function is not defined at that point. In other words, there is a “hole” in the graph of the function at that point. Removable discontinuities can be “fixed” by redefining the function at that point to be equal to the limit.
- Infinite discontinuity:An infinite discontinuity occurs when the limit of the function does not exist. In other words, the graph of the function approaches infinity at that point.
Analyzing Functions for Continuity
To analyze a function for continuity at a given point, follow these steps:
- Find the limit of the function as x approaches that point.
- Evaluate the function at that point.
- If the limit exists and is equal to the value of the function at that point, then the function is continuous at that point.
- If the limit does not exist or is not equal to the value of the function at that point, then the function is discontinuous at that point.
Applications of Continuity
Continuity is an important concept in mathematics, as it is used in a variety of applications, including calculus and optimization.
In calculus, continuity is used to define the derivative of a function. The derivative of a function is a measure of how quickly the function is changing. If a function is not continuous at a point, then its derivative does not exist at that point.
In optimization, continuity is used to find the maximum and minimum values of a function. If a function is not continuous, then it may not have a maximum or minimum value.
Visualizing Continuity
The graph of a continuous function is a smooth curve. There are no breaks or jumps in the graph. The graph of a discontinuous function may have breaks or jumps in it.
| Continuous Function | Discontinuous Function |
|---|---|
 |
 |
Answers to Common Questions: Which Of The Functions Graphed Below Is Continuous
What is a continuous function?
A continuous function is a function whose graph can be drawn without lifting the pen from the paper. In other words, there are no breaks or jumps in the graph.
What are the different types of discontinuities?
There are three main types of discontinuities: jump discontinuities, removable discontinuities, and infinite discontinuities.
How do I determine if a function is continuous at a given point?
To determine if a function is continuous at a given point, you need to check three things: the function is defined at that point, the limit of the function as the input approaches that point exists, and the limit of the function as the input approaches that point is equal to the value of the function at that point.